From June 3rd to June 6th, I participated in the 10th Theory and Practice of Multiparty Computation Workshop (TPMPC 2024), which was held at TU Darmstadt, Germany[TPMPC2024]. Darmstadt is a beautiful and historical city, covered in green plants and immersed in an artistic atmosphere. The workshop was wonderful, and the talks were excellent. I was inspired and the presentations sparked a lot of ideas. On the last day of TPMPC, I was captivated by an amazing talk by Marc Rivinius, on a work with his team at the University of Stuttgart. The title of the talk was 'Optimizing Preprocessing for Maliciously Secure MPC: Faster Matrix Multiplications and Convolutions without Sacrifice'.

After the talk, I found their paper 'Convolutions in Overdrive: Maliciously Secure Convolutions for MPC' for further learning [RRHK23]. It is also remarkable and inspired me to share their work and ideas here.

1 What is Privacy-Preserving Machine Learning?

Privacy preservation is crucial in machine learning. With the increasing adoption of machine learning across a wide variety of application domains, the use of huge volumes of data raises serious privacy concerns, posing high potential risks of leakage for highly sensitive information. Therefore, as a PhD student in Secure multiparty computation (MPC), I closely follow the state-of-the-art advancements and aim at developing better MPC algorithms tailored for specific machine learning models to improve their privacy. Protecting the confidentiality of data is core to MPC researchers' mission. It is also the essential target of Marc's talk.

The talk consisted of 5 parts: Convolutions, Maliciously Secure multiparty computation, Beaver Triples, How to generate Bevear Triples and Sacrificing. Here I will follow the logic of Marc's talk with extra materials from their paper [RRHK23] to share what they have done and what I learned.

2 Convolutions

The talk starts with a discussion on Convolutions, as they concentrate on the optimization of (tensor) convolutions.

Convolution is fundamental in signal processing, computer vision, and machine learning. It applies a filter or kernel to an input image or signal and extracts relevant features. Typical implementations use a sliding-window operation where the kernel moves across the input image. However, this approach can be computationally expensive, especially for large images and kernels. An alternative is to compute convolution as matrix multiplication, which can be a more efficient approach [Bae24]. As shown in Fig.2, the process involves matrix multiplication for one convolution.

Matrix Construction of a \(2D\) Convolution [Bae24]:

Let \(\mathbf{A}\) be a matrix of size \({n}\times{n}\) and \(\mathbf{K}\) a \({k}\times{k}\) kernel. For convenience, let \({t=n-k+1}\).

To calculate the convolution \({\mathbf{A}}\ast{\mathbf{K}}\), we need to calculate the matrix-vector multiplication \({\mathbf{M}}v^{T}={v'}^{T}\) where:

(1) \(\mathbf{M}\) is a \({t^2}\times{n^2}\) block matrix we get from the kernel \(\mathbf{K}\).

(2) \(v\) is a row vector with the \(n^2\) elements of \(\mathbf{A}\) concatenated row by row.

(3) \(v^{'}\) is a row vector of \(t^2\) elements which can be reshaped into a \({t}\times{t}\) matrix by splitting the row vector into \(t\) rows of \(t\) elements.

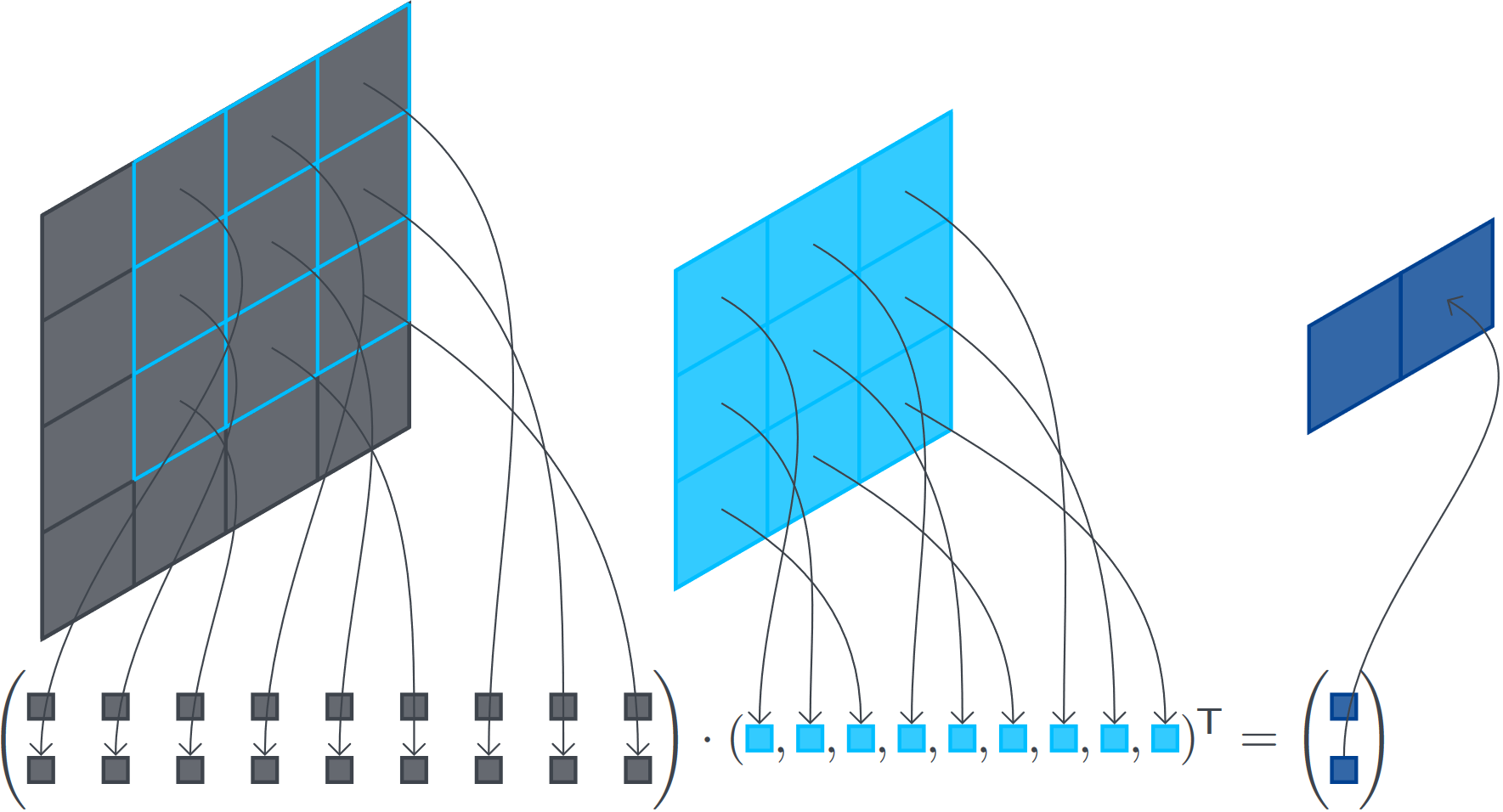
Convolutions are the most commonly used components in the ML architectures, especially in convolutional neural networks but also in recurrent neural networks or transformers, and therefore have a major impact on the overall performance. The difference from previous works is that Rivinius et al. [RRHK23] introduce the first actively secure MPC protocol with direct support for convolutions.

They present three new and more efficient packing methods for convolutions which do not use ciphertext rotations or maskings. The first method is the simple convolution packing, which is based on multidimensional packing with two additional dimensions [BKH+21], [HjLHD22]. The second method is the generalization of Huang et al.'s convolution packing [HjLHD22]. The third method is the depthwise convolution packing, it is the first packing method for depthwise convolutions and can be realized with only homomorphic polynomial multiplications.

3 Maliciously Secure MPC

Maliciously MPC refers to cryptographic protocols enabling multiple parties to jointly compute a function, such as evaluating an ML model over their inputs, while maintaining input privacy even in the presence of malicious adversaries. An adversary, in general, can be semi-honest, following the protocol but seeking additional information, or malicious, deviating from the protocol to gain an advantage. The primary security goals are to ensure the correctness of the result (or to abort if security is compromised) and to keep the inputs of honest parties confidential.

A well known maliciously secure MPC protocol is SPDZ [DPSZ12]. SPDZ is an efficient protocol designed for arithmetic circuits and consists of two main phases: the preprocessing phase and the online phase.

The preprocessing phase is independent of the inputs - that is the reason why it also called offline phase - and responsible for generating a large amount of cryptographic materials such as Beaver triples, random shares, and Message Authentication Codes (MACs). This phase is computationally intensive but can be done offline before the actual inputs are known.

The online phase uses the precomputed materials from the preprocessing phase to perform the actual computation on the inputs. Parties input their private data and perform computations, while ensuring privacy and correctness through the use of MACs. This phase can be highly efficient since most of the heavy lifting is done in the preprocessing phase.

SPDZ has several well-known features: Beaver triples, MACs, Secret Sharing and Sacrificing. Beaver triples are a set of secret shared values \(([\![{a}]\!], [\![{b}]\!], [\![{c}]\!])\) where \(a,b\) are uniformly random and \(c=ab\). These triples are used to ensure that multiplication can be done securely without revealing the private inputs of the parties. Sacrificing is a technique used to verify the correctness of Beaver triples. It involves generating additional triples and using them to check the integrity of the original triples. Additionally, MACs and secret sharing are also core techniques in \(SPDZ\), used for preserving privacy.

4 Beaver Triples

Rivinius et al. [RRHK23] introduce a new efficient convolution triple generation protocol as part of their offline phase. They present two different generation methods: one based on Linear Homomorphic Encryption (LHE), which is presented in a specific subprotocol \({\Pi}_{Offline-LHE}\); and the other based on Somewhat Homomorphic Encryption (SHE), which is presented in another subprotocol \({\Pi}_{Offline-SHE}\). In this section, I will first briefly introduce Beaver multiplication and then outline the LHE-based and SHE-based convolution triple generation methods. Most of the information is taken from the work of Rivinius et al. [RRHK23]. For further details, please refer to their paper.

4.1 Beaver Multiplication

To multiply two shares \({[\![{x}]\!]}_i\), \({[\![{y}]\!]}_i\), one can no longer only perform local operations on shares. Instead, Beaver's multiplication technique is used. Given a triple \(({[\![{a}]\!]}_i, {[\![{b}]\!]}_i, {[\![{c}]\!]}_i)\) with \(c:=ab, u:=x-a, v:=y-b\), we can compute a share of the product as: \({[\![{xy}]\!]}_i={[\![{c}]\!]}_i+v{[\![{a}]\!]}_i+u{[\![{b}]\!]}_i+uv\).

The values \(u\) and \(v\) are obtained by reconstruction of the shares \({[\![{x}]\!]}_i-{[\![{a}]\!]}_i, {[\![{y}]\!]}_i-{[\![{b}]\!]}_i\) where the correctness of the openings is guaranteed by the MAC check. The Beaver triple multiplication can be generalized to arbitrary bilinear operations, i.e., we can replace the multiplication by other bilinear operations like matrix multiplications or convolutions [CKR+20], [MZ17].

Given a convolution triple \(({[\![{a}]\!]}_i, {[\![{f}]\!]}_i, {[\![{c}]\!]}_i)\) for uniformly random \(a,f\) and \(c=conv2d(a,f)\), we can compute a maliciously secure convolution of a secret-shared image \({[\![{x}]\!]}_i\) and a filter \({[\![{y}]\!]}_i\) as a linear combination of the triple and opened values \(u:=x-a,v:=y-f\).

4.2 LHE-based convolution triple generation

Protocol \({\Pi}_{Offline-LHE}\) presents the convolution triple generation based on LHE.

(1) Parties first generate their shares for \(a\) and \(f\). One of them will be proved correctness via ZKPs, and then these shares are sent to all parties.

(2) The parties can multiply these ciphertexts with their own share of \(f\) to obtain ciphertexts of pairwise shares. These pairwise shares will be re-randomized and then sent back to the party who originally sent the encrypted share and holds the corresponding private key.

(3) After receiving all encrypted pairwise shares, this party can decrypt them and combine them to obtain a share of the overall product of packings, e.g., an encoding of the convolution of \(a\) and \(f\).

(4) Finally, all shares are authenticated.

4.3 SHE-based convolution triple generation

Protocol \({\Pi}_{Offline-SHE}\) presents the convolution triple generation based on SHE. It is similarly to protocol \({\Pi}_{Offline-LHE}\), I will not explain the details here, but I refer the reader to the original paper.

5 Sacrificing

Rivinius et al. [RRHK23] use sacrificing to ensure that the produced triple is correctly authenticated. However, the efficiency of the sacrificing greatly depends on the type of bilinear operation considered. The reason for this is the inherent asymmetry of the optimized sacrificing of MASCOT [KOS16] (compared to the original technique used in SPDZ [DPSZ12]). This is especially true for LowGear-style protocols that only require expensive ZKPs for one of the triple elements.

In general, one of the triple inputs (i.e., \(a\) or \(f\) of a triple \((a,f,c)\)) might be more expensive to compute. Therefore, one should consider a reversed version of the sacrificing presented in Fig.3 taking shares of \({a,a',f,c,c'}\) instead. Technically, this can be achieved by using \((op'(y,x)=op(x,y), {[\![{f}]\!]}_i, {[\![{a}]\!]}_i, {[\![{a'}]\!]}_i, {[\![{c}]\!]}_i, {[\![{c'}]\!]}_i)\) as inputs to sacrifice.

6 Conclusion

In a nutshell, Rivinius et al. [RRHK23] proposed an improved protocol that directly supports convolutions. They achieved this by generating convolution triples, rather than using matrix triples as previous works did. This is a significant improvement, and I will continue to follow their future work closely.

Beyond the academic content, I would like to share a photo from a park in Darmstadt, as shown in Fig.4.

The outstanding and humble peers, talented predecessors, enthusiastic organizers, and the beautiful sky, trees, and historical monuments made my first academic event experience unforgettable. Thanks to my dear supervisor, the organizing committee, and the kind lady who introduced Darmstadt to me. I am always so lucky. I hope to attend next year's TPMPC presenting also my own paper!

7 References

[Bae24]Baeldung, 2024. Reviewed by: Milos Simic. 2D Convolution as a Matrix-Matrix Multiplication.

[BKH+21]Song Bian, Dur-E-Shahwar Kundi, Kazuma Hirozawa, Weiqiang Liu, and Takashi Sato. APAS: Application-Specific Accelerators for RLWE-Based Homomorphic Linear Transformations. In Inf. Forensics Secur, volume 16, page 4663–4678. IEEE Trans, 2021.

[CKR+20]Hao Chen, Miran Kim, Ilya Razenshteyn, Dragos Rotaru, Yongsoo Song, and Sameer Wagh. Maliciously Secure Matrix Multiplication with Applications to Private Deep Learning. In Advances in Cryptology–ASIACRYPT 2020: 26th International Conference on the Theory and Application of Cryptology and Information Security, Daejeon, South Korea, December 7–11, 2020, Proceedings, Part III 26, pages 31–59. Springer, 2020.

[Dar24]TU Darmstadt. The 10th Theory and Practice of MultiParty Computation Workshop (TPMPC 2024).

[DPSZ12]Ivan Damgard, Valerio Pastro, Nigel P. Smart, and Sarah Zakarias. Multiparty Computation From Somewhat Homomorphic Encryption. In Annual Cryptology Conference, pages 643–662. Springer, 2012.

[HjLHD22]Zhicong Huang, Wen jie Lu, Cheng Hong, and Jiansheng Ding. Cheetah: Lean and Fast Secure Two-Party Deep Neural Network Inference. In In 31st USENIX Security Symposium, USENIX Security 2022, volume 16, page 809–826. USENIX Association, 2022.

[KOS16]Marcel Keller, Emmanuela Orsini, and Peter Scholl. MASCOT: Faster Malicious Arithmetic Secure Computation with Oblivious Transfer. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pages 830–842, 2016.

[MZ17]Payman Mohassel and Yupeng Zhang. Secureml: A System for Scalable Privacy-preserving Machine Learning. In 2017 IEEE Symposium on Security and Privacy (SP), pages 19–38. IEEE, 2017.

[RRHK23]Marc Rivinius, Pascal Reisert, Sebastian Hasler, and Ralf K¨usters. Convolutions in Overdrive: Maliciously Secure Convolutions for MPC. Proceedings on Privacy Enhancing Technologies, 2023.